‘Tractography’ is a brain imaging technique that broadly describes the mapping of the location and direction of white matter bundles and their constituent fibers within the human brain1.
Conventionally, tractography is achieved using an imaging model called diffusion tensor imaging (DTI). However, due to limitations in resolving more complex white matter structures found in often critical functional networks of the human brain, such as the sensorimotor system, a more advanced algorithm known as constrained spherical deconvolution (CSD) is seeing increasing use in current neuroimaging toolsets, including Omniscient's Quicktome platform.
The basis of tractography is to measure the diffusion of water molecules in the brain to detect the locations of white matter fibers. Generally, water will more easily diffuse along the direction of white matter tracts2,3, and thus such data can be harnessed to generate three-dimensional structural maps of the brain's connectomic networks.
This is achieved non-invasively by performing diffusion-weighted imaging (DWI), a variant of conventional magnetic resonance imaging (MRI) that measures the rate of tissue water diffusion. Combining this data with modeling algorithms, such as DTI or CSD, then allows for the inference of diffusion direction(s) in each cubic region, or voxel, of the brain.
Figure 1. Whole brain tractography generated through Constrained Spherical Deconvolution (CSD).
.png?width=1600&height=1080&name=Image_%20Hero-Corticospinal-Parcels%20(A).png)
Figure 2. Mid-coronal schematic of white and gray matter divisions within the human cerebrum. Colored cubes indicate independent functional gray matter regions (parcels), and colored lines the white matter tracts which connect them. This figure was generated in o8t Quicktome software
DWI collection involves setting a pre-determined number of gradient directions. That is, how many different angles within a 360-degree circle will water molecules be stimulated. For example, a DWI collection with 12 gradient directions will measure the diffusivity of water on every 30 degree angle, whereas a 32 gradient direction scan will measure every 11.25 degrees4.
Generally, increasing the number of gradient directions improves the reliability of generating accurate tractography5 As previously mentioned, water molecules exhibit a high diffusivity rate along an axon, and as such the angle which generates the highest diffusivity rate within a given voxel suggests that this is the direction of white matter structures within that voxel2,3.
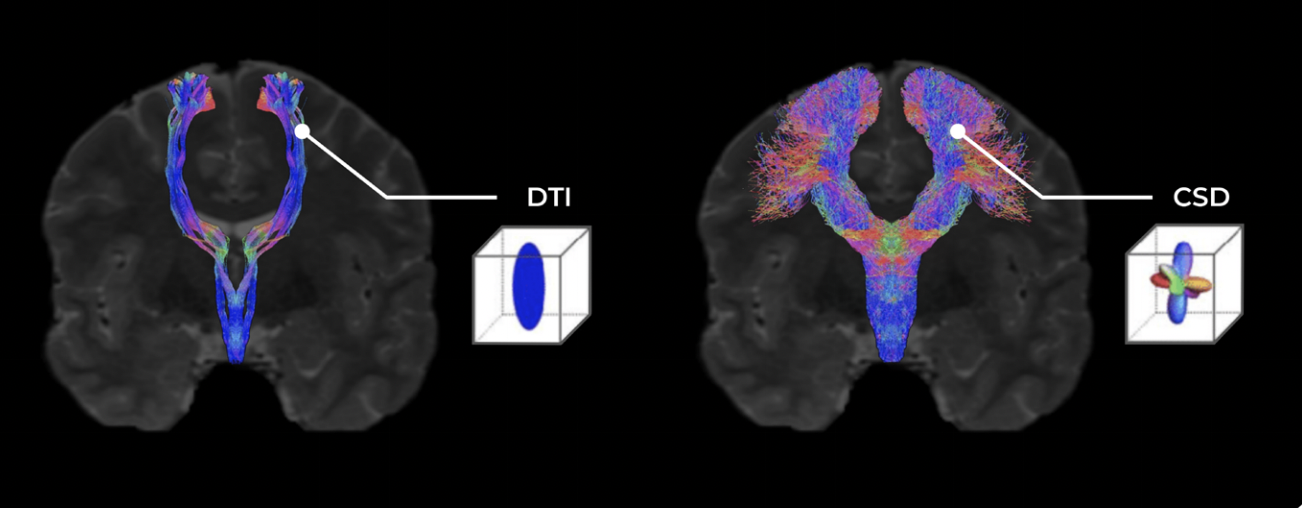
Imagine white matter tracts as the highways which connect the brain's major cities, or in this case, functional gray matter regions together. Previous and conventional methods of resolving DWI, such as DTI, considered these highways as spatially independent, connecting two cities together as a single road. However, highways typically also involve off-ramps, overpasses, and adjacent streets in close proximity. White matter structures within the cortex too hold greater complexity that cannot be accurately represented by a single directional value.
The primary limitation of previous techniques is that only one value, or tensor, representing the average direction of white matter tracts within a cubic voxel was able to be generated3,6. Whilst this assumption may enable the visualization of larger structures such as the Arcuate Fasciculus of the language system and Spinothalamic Tract of the sensorimotor system, it neglects that many smaller white matter structures originate as branches from or cross paths with these major structures, and would therefore be averaged out by the overarching diffusivity direction within voxels where an overlap is present6.
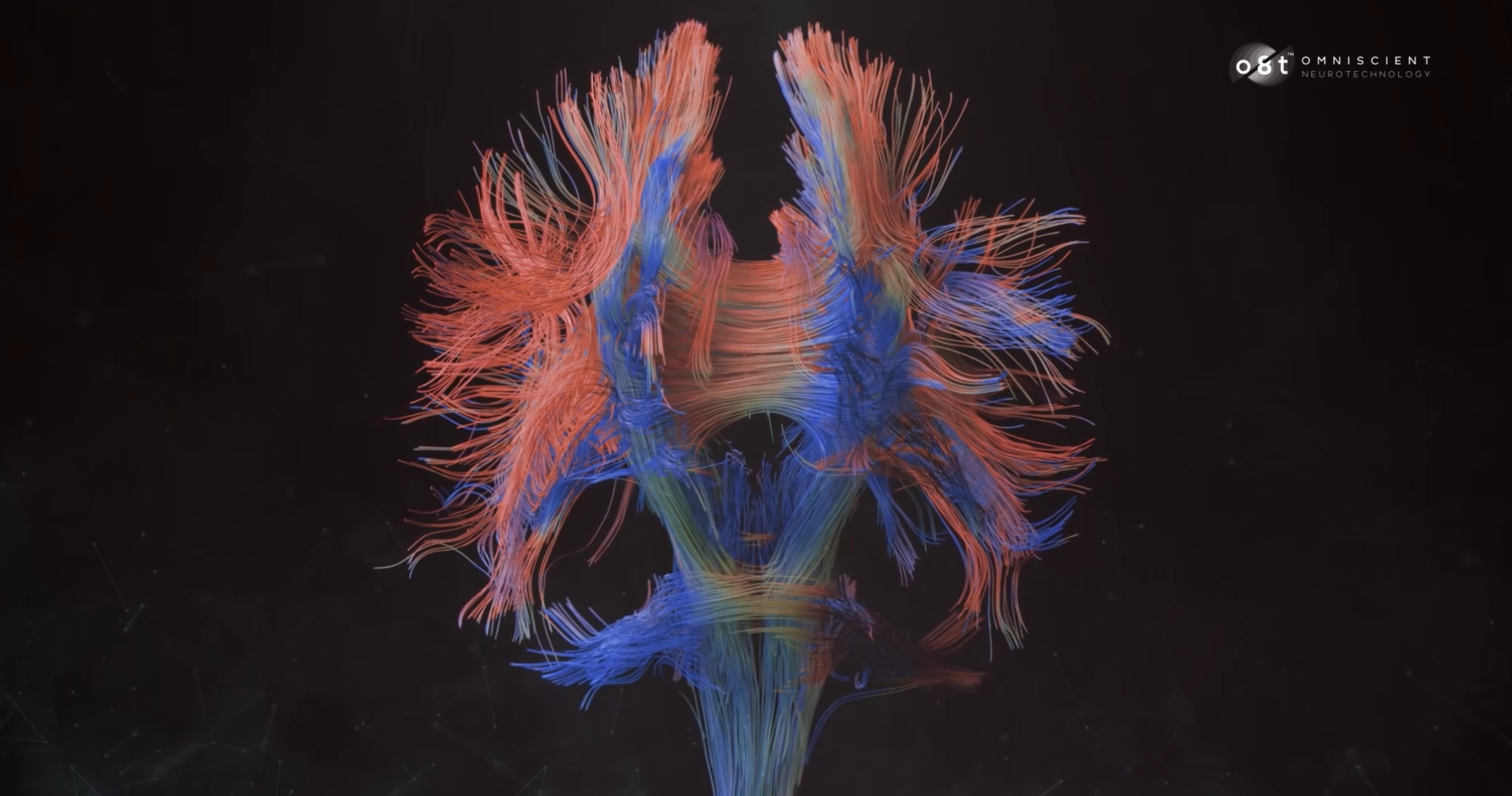
Arguably the greatest challenge in tractography analyses to date is resolving these high-density regions of white matter which include a number of crossing or touching fibers. Whilst a number of techniques have been developed to address this issue, the most superior, yet computationally demanding solution is “Constrained Spherical Deconvolution” (CSD).
Instead of an ‘average water diffusivity' value, CSD tractography generates a ‘fiber orientation distribution’ value for each voxel of neural tissue collected in the DWI series. This distribution value instead provides information on: a) the dominant diffusion signal within a voxel (major tracts), b) other independent direction signals also present within a voxel (fibers that cross under or above the dominant tract, and c) diffusion signals which branch from the dominant signal (fibers which branch or make contact with the major tract)7-9.
%20(1).png?width=748&height=421&name=CSD%20(1)%20(1).png)
Figure 3: The many situations in which complex fiber orientations arise in the brain11. Situations such as crossing fibers, branching and fanning require a more robust fiber orientation model to accurately represent and construct tractography with.
As described above, CSD generates for each voxel of neural tissue within the DWI scan a value describing the orientation and distribution of all white matter fibers within it.
The steps following the calculation of this value allow for these fibers to then be tracked through adjacent sections of tissue until they reach a termination point - either at a synaptic junction or at gray matter tissue which they likely innervate. This process is known as “streamlining” and involves setting stopping criteria, from which CSD algorithms can sort through adjacent white matter tissue, track the course of white matter fibers and halt their mapping once these criteria are met10. Critically, this process generates a complete and further refined view for investigating the complete course of individual white matter tracts and larger bundles than can be generated by standard DTI techniques10,11.
An important and clinically relevant application of CSD is in the case of brain cancer research, where the site of a present or resected tumor has caused a shift in adjacent white and gray matter structures surrounding it. In these instances, CSD has shown considerable advantage over DTI in resolving how the course of white matter tracts has been disturbed, and is further able to effectively map the new paths of major bundles and individual fibers which has major implications for both neurosurgical planning and subsequent treatment strategy11,12.
Figure 4 : A comparison of outputs between DTI (on the left) and CSD (on the right) in modelling the fiber response and reconstructing the Corticospinal Tract. The DTI model only assumes one direction per model by extracting its eigenvector while the CSD algorithm handles multiple crossing fibers per voxel.
Roughly 70-90% of white matter voxels within the human cortex contain multiple fiber orientations either due to crossing, branching or touching fibers and thus conventional DTI may be unsuited for applications of tractography that demand precision13. CSD tractography represents a significant methodological improvement when investigating small white matter structures within the brain. Whilst the iterative process of CSD makes it a computationally demanding method to perform, current research into machine-learning based approaches to CSD by leveraging cloud computing and parallel processing are driving the production of more efficient algorithms to generate accurate tractography.
© o8t 2024 | Privacy Policy
